How succinct proofs leak information
What happens when a succinct proof does not have the zero-knowledge property? There is a common misconception that “succinct proofs are too short to leak information about the witness”. This is wrong and in the interest of privacy it is very important that we challenge this belief. The Zeitgeist puzzle at ZK Hack V was based on the themes discussed here.
In this post I’ll present what I am calling a “chosen-instance attack”. Reminiscent of chosen-plaintext attacks for encryption schemes, a chosen-instance attack is a concrete procedure that allows an adversary to steal private inputs from an honest SNARK prover. As we will see in this article, the adversary will request multiple proofs from the prover for instances that are distinct but share the same witness. Given the prover’s responses, the adversary can interpolate a polynomial that encodes the witness. Beyond the technical description of the attack, we’ll also discuss how this scenario can arise very naturally in deployed systems.
Throughout, I’ll assume that readers have some familiarity with succinct proofs, including notions such as “$\mathsf{NP}$ relations”, “instance”, “witness”, “SNARK” and “IOP”/”polyIOP”. As a quick primer, you can read “$\mathsf{NP}$ relation” to mean circuit, “instance” to mean public inputs, “witness” to mean private inputs and intermediate computation steps/wires; “SNARKs” are our beloved succinct proofs and “IOP”/”polyIOP” are their primary building blocks. For a more complete introduction, I suggest you either check out the Introduction to ZK Jargon, Module 1 of the ZK Whiteboard Sessions or the Chiesa and Yogev textbook [CY24].
Threat model
We focus on non-interactive proof (or argument) systems and consider the following threat model. An adversary $\mathcal{A}$ knows the public inputs to a circuit and interacts with an honest prover $P$ who knows all the other wire values (private inputs and any intermediate computation steps). The adversary can adaptively request proofs from the prover for any public inputs of its choosing. Eventually, the adversary must output the prover’s secret wire values.
Restating the above formally: for any $\mathsf{NP}$ relation $\mathcal{R}$, the prover is given an instance-witness pair $(x,w) \in \mathcal{R}$ and the adversary is given $x$. The adversary is adaptive and has black-box oracle access1 to the honest prover’s output function. The chosen-instance attack is successful if $\mathcal{A}$ outputs $w$ with better than negligible probability. The threat model is illustrated in Figure 1 below.
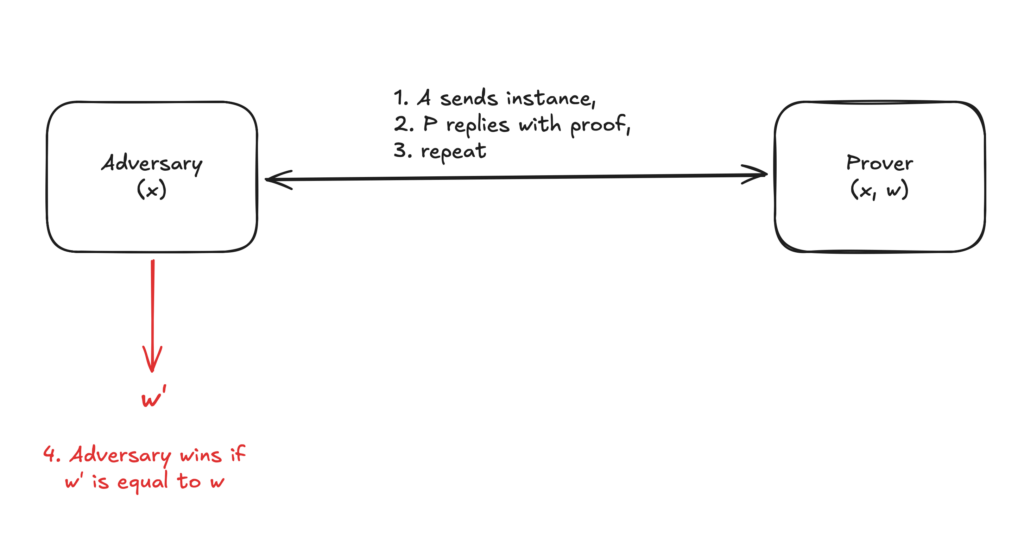
This setting is very common in the wild. For example, in applications that require client-side proofs, the user’s device is the honest prover and the application server can act as the adversary. This is the setting we chose for the ZK Hack puzzle. Alternatively, we could imagine an untrusted server that produces proofs to convince clients of its honesty. A malicious client could try to extract secrets from the server by choosing the statements the server will prove.
Leaky primitives
IOPs. Most modern SNARKs are built from interactive oracle proofs (IOP) or their polynomial variants (polyIOP). The general pattern is the following:
- Round 1: the prover sends an oracle that, in the honest case, is a polynomial encoding the witness2.
- Round $i$: the prover sends a “helper” oracle that will allow the verifier to reduce the task of checking properties of the witness to a simpler task.
- Final round: the verifier queries the witness and helper oracles in one or more random points.
This construction leaks at least one evaluation of the witness polynomial by default. If the witness is encoded into a degree d polynomial, then an adversary can collect $d+1$ proofs and use the evaluations to interpolate and recover the full witness polynomial! It is also common for IOPs to check constraints across $k$ adjacent values of the witness polynomial(s). To do so, these protocols require the prover to open $k$ witness values, cutting the number of proofs from $d+1$ to $\frac{d+1}{k}$.
Compilation using polynomial commitments. The generic IOP above is usually compiled into a SNARK in one of the two following ways. The first is to commit to messages using a polynomial commitment scheme and make the protocol non-interactive using the Fiat-Shamir transform. This yields most of our elliptic curve SNARKs and is a process that does not usually leak further witness evaluations3.
Compilation using IOPPs and Merkle trees. The second method is to engage in an additional protocol attesting that the prover’s messages are “close” to polynomials. This is known as an IOP of Proximity (IOPP); popular examples include FRI [BBHR18] and STIR [ACFY24] amongst many others. The combined protocol (IOP + IOPP) is compiled into a SNARK by running the BCS compiler [BCS16]: we commit to each message with a Merkle tree and make the protocol non-interactive using the Fiat-Shamir transform. This yields most of our hash-based SNARKs. The IOPP compilation method leaks additional evaluations of the witness polynomial. Indeed, known IOPPs require the verifier to repeatedly open values of the oracles being tested. Depending on the security regime and chosen parameters, we usually perform between 20 and 50 openings per proof.
Non-interactive proofs
As we have seen, the interactive building blocks for our SNARKs leak evaluations of the witness polynomial. Extracting the prover’s witness in the interactive setting is relatively easy: run the protocol honestly acting as the verifier and make sure that the evaluation points are distinct in every run. After enough runs, interpolate the witness polynomial.
In the non-interactive setting, things are not so simple. Since we have applied the Fiat-Shamir transform, the verifier’s messages — and therefore evaluation points — are computed deterministically from a hash of the instance and previous prover messages. For a fixed instance-witness pair $(x,w)$, an honest prover will always return the same fixed proof, preventing the adversary from obtained multiple evaluations of the witness polynomial.
The solution is to request proofs for many instances $x_1, x_2, \dots, x_n$ such that these instances are all satisfied by the same witness $w$. Depending on the $\mathsf{NP}$ relation, this might not be possible. In the next section, I’ll argue that this condition is naturally met by very common circuits. For now, let’s assume that there exists such a set of instances.
A direct consequence of using different instances is that the verifier messages derived from the hash function will be different in each execution. This will yield distinct evaluation points across proofs as required! However, in doing so we have complicated the adversary’s task. Indeed, in some arithmetizations the prover’s first message is a polynomial that depends on both the witness and the instance. If we use different instances, the prover’s first message will be different every time; seemingly thwarting our interpolation attack.
Fortunately for our attack, there exists a mathematical trick that allows the adversary to separate the witness-part of the polynomial from the instance-part of the polynomial. The idea is to interpret the combined instance-witness polynomial $\tilde z$ as the sum of two polynomials: the first is an adversary-known polynomial $\tilde x$ that depends only on the instance, the second is a polynomial $\tilde w$ that depends only on the witness. Given an evaluation $\tilde z(p)$ of the combined polynomial at a point $p$, the adversary can evaluate $\tilde x(p)$ and compute $\tilde w(p) = \tilde z (p) − \tilde x (p)$. The trick is illustrated below for an R1CS instance-witness polynomial but can equally be applied to a column of a PLONKish or AIR table.
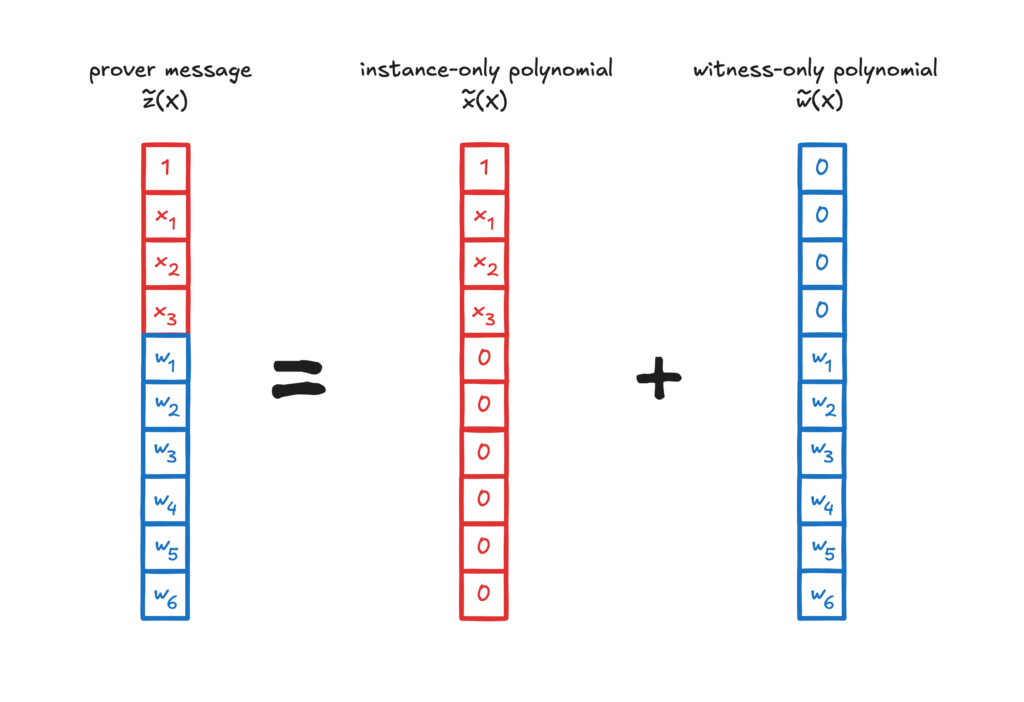
Having recovered at least one evaluation of the witness polynomial per proof, the attack can proceed as before: collect enough proofs and interpolate the witness.
Chosen-instance attacks in the wild
At first, it might seem like the attack we described requires a very contrived circuit: there needs to be many instances that are satisfied by the same witness. Furthermore, the adversary starts with only one of those instance; how does it produce more instances that are satisfied by the fixed witness?
It turns out that many circuits exhibit these properties, in particular when “nonces” or “nullifiers” are involved. When dealing with non-interactive proofs, applications must be careful not to allow proofs to be re-used. For example, if Alice produces a proof that her account balance is above 32 ETH, application designers will want to make sure that she cannot spend some ETH and still present the old proof. This is often done by associating a unique public number (nonce) to the proof. When the proof is verified, the public nonce gets added to a log and the proof is marked as “consumed”. If the same proof is presented once again, the verifier will recognize that the nonce was already added to the log, and therefore that the proof should not be accepted again.
This “nullifying” mechanism is great to reject attempts at replaying a proof, but makes it very natural for a prover to prove many different instances with a single witness. Indeed, instead of checking that the public inputs $x$ and witness $w$ satisfy the circuit, we now have public inputs $(x, \mathsf{nonce})$ and witness $w$. The adversary can keep a fixed $x$ and cycle through many values of $\mathsf{nonce}$; meanwhile the prover is stuck using its fixed witness.
Conclusion
While it is true that a single succinct proof is too short to leak the full witness, it is not true that succinct proofs are enough to guarantee privacy. Most of our succinct proofs leak information correlated to private inputs. As a consequence, even a single proof can act as a unique fingerprint for the witness. This is especially true when the proof contains a commitment to the witness.
In some settings — in particular when using nonces to prevent replay attacks — the leakage can be exploited to mount the chosen-instance attack we described above and fully recover the witness. The attack works against any circuit for which many instances are satisfied by a single witness. It is particularly effective against SNARKs that rely on IOPs of Proximity (e.g., FRI, STIR) since these SNARKs leak a bigger number of evaluations per proof.
The chosen-instance attack is only one idea of how to exploit such leaks; there are surely more that are known, and many more that are yet unknown! Therefore, I’ll conclude this article with a final word of warning at the risk of sounding like a broken record: if a system’s proofs are not zero-knowledge, then the system does not guarantee privacy.
References
[ACFY24] Gal Arnon, Alessandro Chiesa, Giacomo Fenzi, and Eylon Yogev (2024). STIR: Reed-Solomon Proximity Testing with Fewer Queries. In: Reyzin, L., Stebila, D. (eds) Advances in Cryptology – CRYPTO 2024. CRYPTO 2024. Lecture Notes in Computer Science, vol 14929. Springer, Cham. https://doi.org/10.1007/978-3-031-68403-6_12
[BBHR18] Eli Ben-Sasson, Iddo Bentov, Yinon Horesh, and Michael Riabzev. Fast Reed-Solomon Interactive Oracle Proofs of Proximity. In 45th International Colloquium on Automata, Languages, and Programming (ICALP 2018). Leibniz International Proceedings in Informatics (LIPIcs), Volume 107, pp. 14:1-14:17, Schloss Dagstuhl – Leibniz-Zentrum für Informatik (2018). https://doi.org/10.4230/LIPIcs.ICALP.2018.14
[BCS16] Eli Ben-Sasson, Alessandro Chiesa, and Nicholas Spooner (2016). Interactive Oracle Proofs. In: Hirt, M., Smith, A. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9986. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53644-5_2
[CY24] Alessandro Chiesa, and Eylon Yogev (2024). Building Cryptographic Proofs from Hash Functions. Published online https://snargsbook.org
Footnotes
- 1 “Black-box” means that the adversary cannot observe the prover’s program description nor see its internal variables. ↩
- 2 In some IOPs the witness is encoded in more than one polynomial (e.g. Plonk/AIR). The attack procedure will work in the same way for this case, making sure to apply it to each of the witness polynomials. ↩
- 3 For computationally bounded adversaries, assuming that the elliptic curve discrete logarithm problem is hard. ↩
 Skip to content
Skip to content
