Dynamic Pricing for Non-fungible Resources
Public blockchains implement a fee mechanism to allocate scarce computational resources across competing transactions. Most existing fee market designs utilize a joint, fungible unit of account (e.g., gas in Ethereum) to price otherwise non-fungible resources such as bandwidth, computation, and storage, by hardcoding their relative prices. Fixing the relative price of each resource in this way inhibits granular price discovery, limiting scalability and opening up the possibility of denial-of-service attacks.
  • Theo Diamandis,
  • Alex Evans,
  • Tarun Chitra,
  • Guillermo Angeris
  • Basics
 08.16.22
Optimal Routing for Constant Function Market Makers
We consider the problem of optimally executing an order involving multiple cryptoassets, sometimes called tokens, on a network of multiple constant function market makers (CFMMs). When we ignore the fixed cost associated with executing an order on a CFMM, this optimal routing problem can be cast as a convex optimization problem, which is computationally tractable. When we include the fixed costs, the optimal routing problem is a mixed-integer convex problem, which can be solved using (sometimes slow) global optimization methods, or approximately solved using various heuristics based on convex optimization. The optimal routing problem includes as a special case the problem of identifying an arbitrage present in a network of CFMMs, or certifying that none exists.
  • Guillermo Angeris,
  • Tarun Chitra,
  • Alex Evans,
  • Stephen Boyd
  • MEV
 12.01.21
Replicating Monotonic Payoffs Without Oracles
In this paper, we show that any monotonic payoff can be replicated using only liquidity provider shares in constant function market makers (CFMMs), without the need for additional collateral or oracles. Such payoffs include cash-or-nothing calls and capped calls, among many others, and we give an explicit method for finding a trading function matching these payoffs. For example, this method provides an easy way to show that the trading function for maintaining a portfolio where 50% of the portfolio is allocated in one asset and 50% in the other is exactly the constant product market maker (e.g., Uniswap) from first principles. We additionally provide a simple formula for the total earnings of an arbitrageur who is arbitraging against these CFMMs.
  • Guillermo Angeris,
  • Alex Evans,
  • Tarun Chitra
  • DeFi
 09.01.21
Constant Function Market Makers: Multi-Asset Trades via Convex Optimization
The rise of Ethereum and other blockchains that support smart contracts has led to the creation of decentralized exchanges (DEXs), such as Uniswap, Balancer, Curve, mStable, and SushiSwap, which enable agents to trade cryptocurrencies without trusting a centralized authority. While traditional exchanges use order books to match and execute trades, DEXs are typically organized as constant function market makers (CFMMs). CFMMs accept and reject proposed trades based on the evaluation of a function that depends on the proposed trade and the current reserves of the DEX. For trades that involve only two assets, CFMMs are easy to understand, via two functions that give the quantity of one asset that must be tendered to receive a given quantity of the other, and vice versa. When more than two assets are being exchanged, it is harder to understand the landscape of possible trades. We observe that various problems of choosing a multi-asset trade can be formulated as convex optimization problems, and can therefore be reliably and efficiently solved.
  • Guillermo Angeris,
  • Akshay Agrawal,
  • Alex Evans,
  • Tarun Chitra,
  • Stephen Boyd
  • Basics,
  • DeFi
 07.01.21
Replicating Market Makers
We present a method for constructing Constant Function Market Makers (CFMMs) whose portfolio value functions match a desired payoff. More specifically, we show that the space of concave, nonnegative, nondecreasing, 1-homogeneous payoff functions and the space of convex CFMMs are equivalent; in other words, every CFMM has a concave, nonnegative, nondecreasing, 1-homogeneous payoff function, and every payoff function with these properties has a corresponding convex CFMM. We demonstrate a simple method for recovering a CFMM trading function that produces this desired payoff. This method uses only basic tools from convex analysis and is intimately related to Fenchel conjugacy. We demonstrate our result by constructing trading functions corresponding to basic payoffs, as well as standard financial derivatives such as options and swaps.
  • Guillermo Angeris,
  • Alex Evans,
  • Tarun Chitra
  • DeFi
 03.01.21
A Note on Privacy in Constant Function Market Makers
Constant function market makers (CFMMs) such as Uniswap, Balancer, Curve, and mStable, among many others, make up some of the largest decentralized exchanges on Ethereum and other blockchains. Because all transactions are public in current implementations, a natural next question is if there exist similar decentralized exchanges which are privacy-preserving; i.e., if a transaction’s quantities are hidden from the public view, then an adversary cannot correctly reconstruct the traded quantities from other public information. In this note, we show that privacy is impossible with the usual implementations of CFMMs under most reasonable models of an adversary and provide some mitigating strategies.
  • Guillermo Angeris,
  • Alex Evans,
  • Tarun Chitra
  • Privacy
 02.01.21
Optimal Fees for Geometric Mean Market Makers
Constant Function Market Makers (CFMMs) are a family of automated market makers that enable censorship-resistant decentralized exchange on public blockchains. Arbitrage trades have been shown to align the prices reported by CFMMs with those of external markets. These trades impose costs on Liquidity Providers (LPs) who supply reserves to CFMMs. Trading fees have been proposed as a mechanism for compensating LPs for arbitrage losses. However, large fees reduce the accuracy of the prices reported by CFMMs and can cause reserves to deviate from desirable asset compositions. CFMM designers are therefore faced with the problem of how to optimally select fees to attract liquidity. We develop a framework for determining the value to LPs of supplying liquidity to a CFMM with fees when the underlying process follows a general diffusion. Focusing on a popular class of CFMMs which we call Geometric Mean Market Makers (G3Ms), our approach also allows one to select optimal fees for maximizing LP value. We illustrate our methodology by showing that an LP with mean-variance utility will prefer a G3M over all alternative trading strategies as fees approach zero.
  • Guillermo Angeris,
  • Tarun Chitra,
  • Alex Evans,
  • Stephen Boyd
  • DeFi
 01.04.21
Liquidity Provider Returns in Geometric Mean Markets
Geometric mean market makers (G3Ms), such as Uniswap and Balancer, comprise a popular class of automated market makers (AMMs) defined by the following rule: the reserves of the AMM before and after each trade must have the same (weighted) geometric mean. This paper extends several results known for constant-weight G3Ms to the general case of G3Ms with time-varying and potentially stochastic weights. These results include the returns and no-arbitrage prices of liquidity pool (LP) shares that investors receive for supplying liquidity to G3Ms. Using these expressions, we show how to create G3Ms whose LP shares replicate the payoffs of financial derivatives. The resulting hedges are model-independent and exact for derivative contracts whose payoff functions satisfy an elasticity constraint. These strategies allow LP shares to replicate various trading strategies and financial contracts, including standard options. G3Ms are thus shown to be capable of recreating a variety of active trading strategies through passive positions in LP shares.
  • Alex Evans
  • DeFi
 06.01.20
Back

Multi-dimensional On-chain Resource Pricing

08.16.22

Public blockchains allow any user to submit transactions which modify the shared state of the network. These transactions are independently verified and executed by a decentralized network of full nodes. Because full nodes have limited computational resources, blockchains limit the total computational resources that can be consumed per unit of time. As user demand may fluctuate, most blockchains implement a transaction fee mechanism in order to allocate finite computational capacity among competing transactions.

The problem

Most existing fee market designs utilize a joint, fungible unit (called gas in Ethereum) to price otherwise non-fungible resources (such as bandwidth, computation, and storage) by hardcoding their relative prices. These one-dimensional fee markets fix the relative price of each resource, which inhibits granular price discovery, opens up the possibility of denial-of-service attacks, and limits scalability as resource needs may change dramatically but the relative prices stay fixed.

To address these issues, many prominent networks such as Ethereum and Solana have proposed multi-dimensional fee markets. In our most recent paper, we provide a principled way to design fee markets that efficiently price multiple non-fungible resources. Importantly, our fee mechanism unifies the competing objectives of the transaction producers (e.g., to maximize their own profit) and of the blockchain designer (e.g., to achieve a target network throughput). Furthermore, our framework provides a precise way to reason about tradeoffs between these competing objectives.

The characters

Blockchain users: Users submit transactions that they want executed on chain. Transactions provide some amount of utility for the user, which may be measurable (for instance, in MEV) or unmeasurable. To ensure their transactions are executed, users must pay fees to the network (for example, the amount burned in EIP-1559) and to the block builders (the tip).

Blockchain validators: Validators run full nodes that verify transactions submitted to the chain. For providing this service, validators are often rewarded by tips, paid by the users, and by rewards from the network. Thus, each transaction that is included provides some utility to the validators, which is a function of the transaction itself, the tips from the transaction, and the computational resources required to validate the transaction.

Blockchain designers: Blockchain network designers aim to maximize the throughput of their network, subject to the hardware specs of the full nodes. The designer sets the full node minimum requirements in a way that balances decentralization and throughput, as lower requirements limit throughput but allow more people to run full nodes for the network. The network designer also may set a resource limit for each block. (For example, in Ethereum, blocks have a gas limit of 30M.) The limit ensures a full node meeting the minimum hardware requirements can reconstruct and verify the current state of the chain (i.e., that full nodes meeting the minimal spec can catch up to the end of the chain in a reasonable amount of time).

In our work, we group the validators and users into one group: the transaction producers. This group has some aggregate utility function of the included transactions and must pay fees to the network in order to include these transactions. Block space markets emerge between the transaction producers, who aim to maximize utility, and the blockchain designers, who aim to maximize the throughput of the network, subject to the minimum hardware requirements.

The mechanism

We start by modeling the resource pricing problem as one in which an omniscient network designer chooses transactions for each block that maximize total welfare subject to demand constraints. Of course, welfare is unknown and likely unmeasurable by the network designer in practice. We show that this problem, which is the ‘ideal end state’ of a blockchain but not immediately useful in itself, decomposes into two problems, coupled by the resource prices. One of these two problems is a simple one which can be easily solved on chain and represents the cost to the network for providing certain resources, while the other is a maximal-utility problem that miners and users implicitly solve when creating and including transactions for a given block. Correctly setting the resource prices aligns incentives such that the resource costs to the network are exactly balanced by the utility gained by the users and miners. This, in turn, leads to block allocations which solve the original ‘ideal’ problem, on average.

The cost of uniform prices

While our paper is mostly theoretical, we also examine a toy model of a blockchain with two resources. We show that pricing resources using our method can increase network efficiency and make the network more robust to DoS attacks or distribution shifts.

Steady-state behavior

We first simulate the steady state behavior of our mechanism with transactions that require roughly equal amounts of resource 1 and resource 2 (e.g., compute and storage).

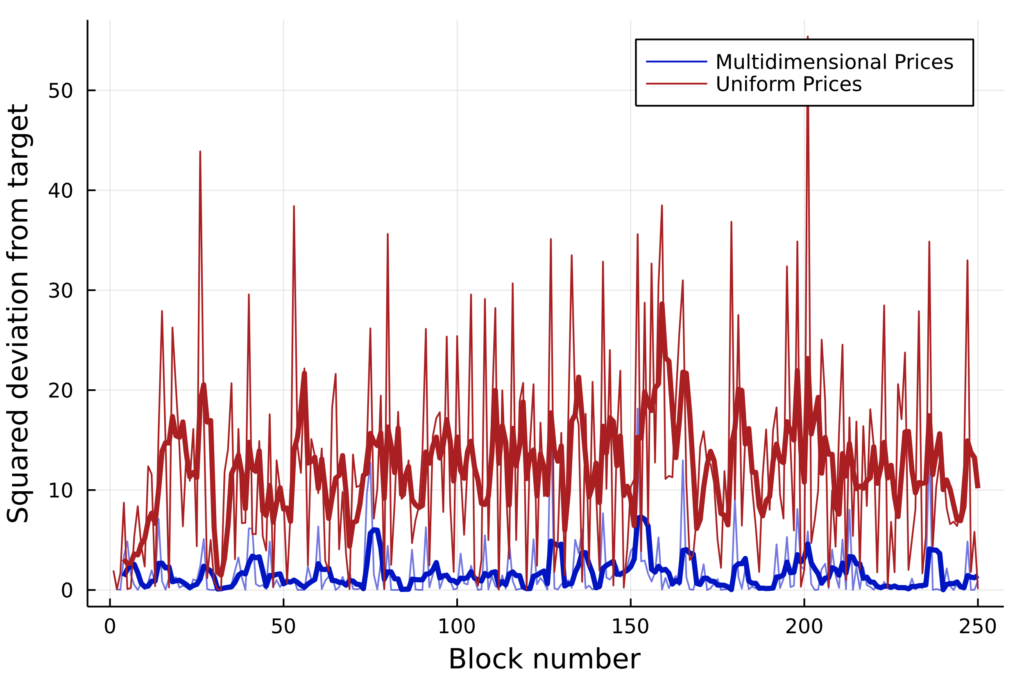
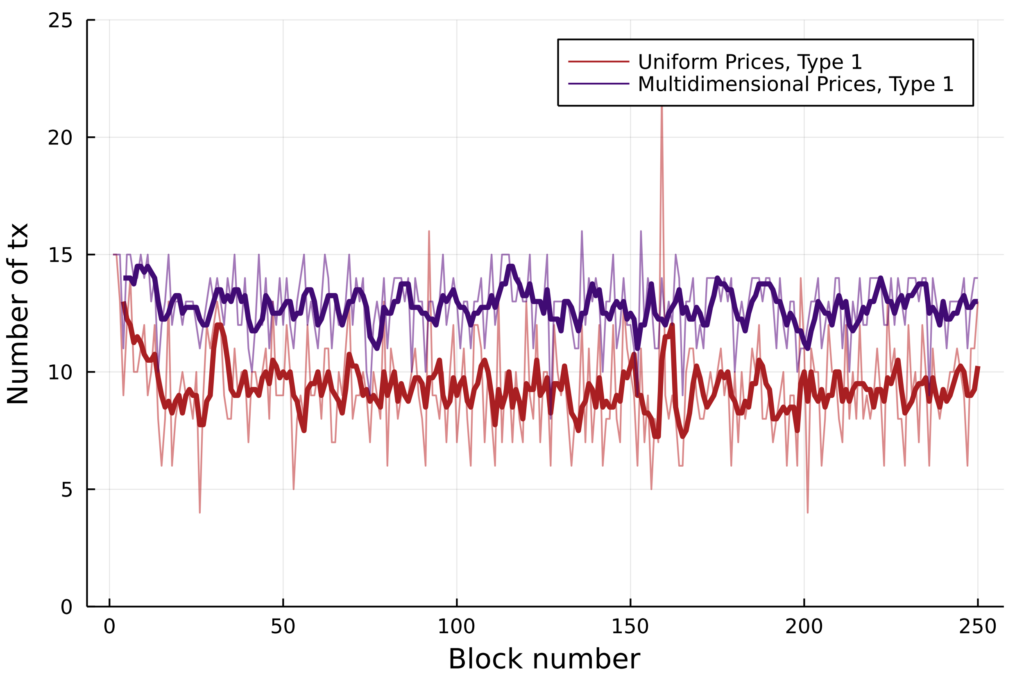
Under steady state behavior, uniform pricing causes higher deviation from resource usage targets (left). This less efficient usage of resources, in the uniform case, also leads to lower throughput (right).

Distribution shifts

We also test mechanism behavior under a distribution shift: we add 150 transactions in block 10 that require a significant amount of resource 2 (e.g., storage). This scenario may appear in an NFT mint, for example.

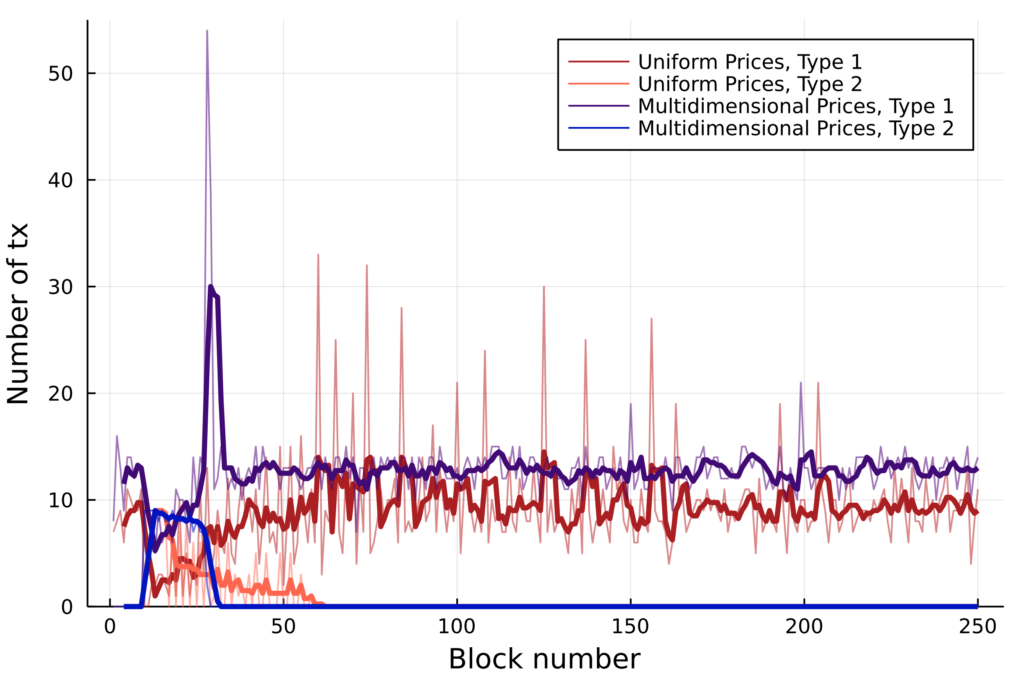
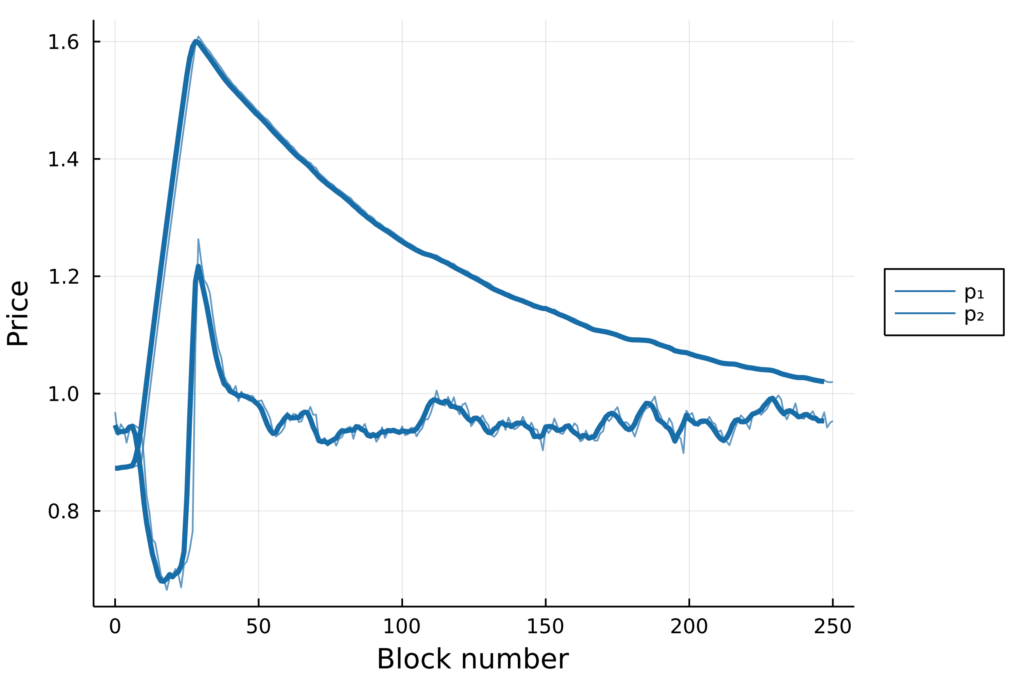
Multidimensional pricing also leads to significantly higher throughput when the distribution shifts (left) by adjusting resource prices accordingly (right).

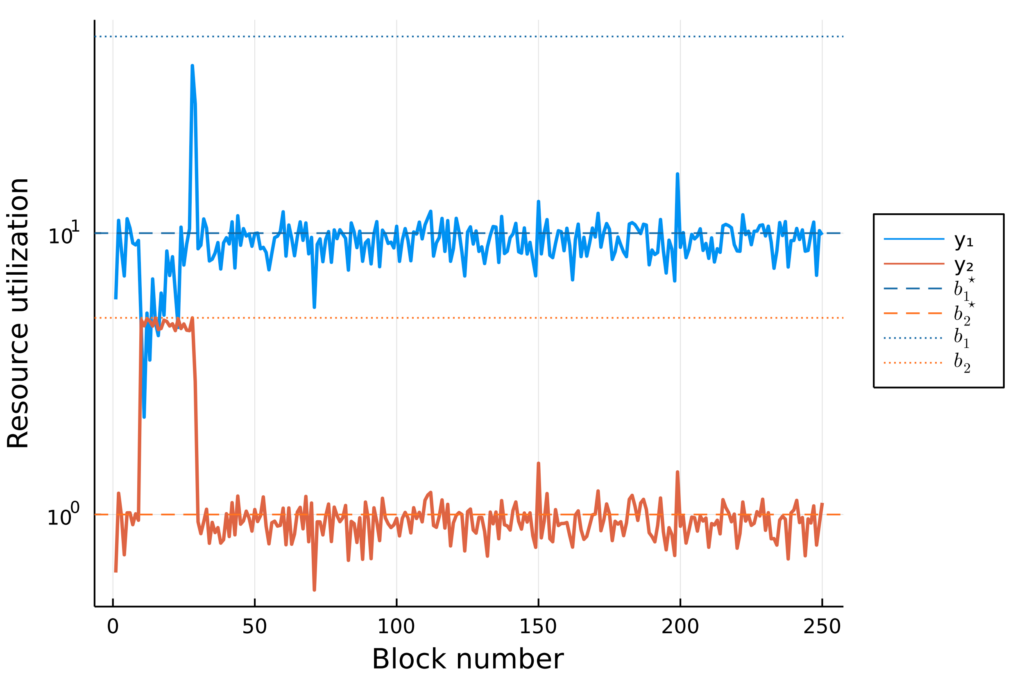
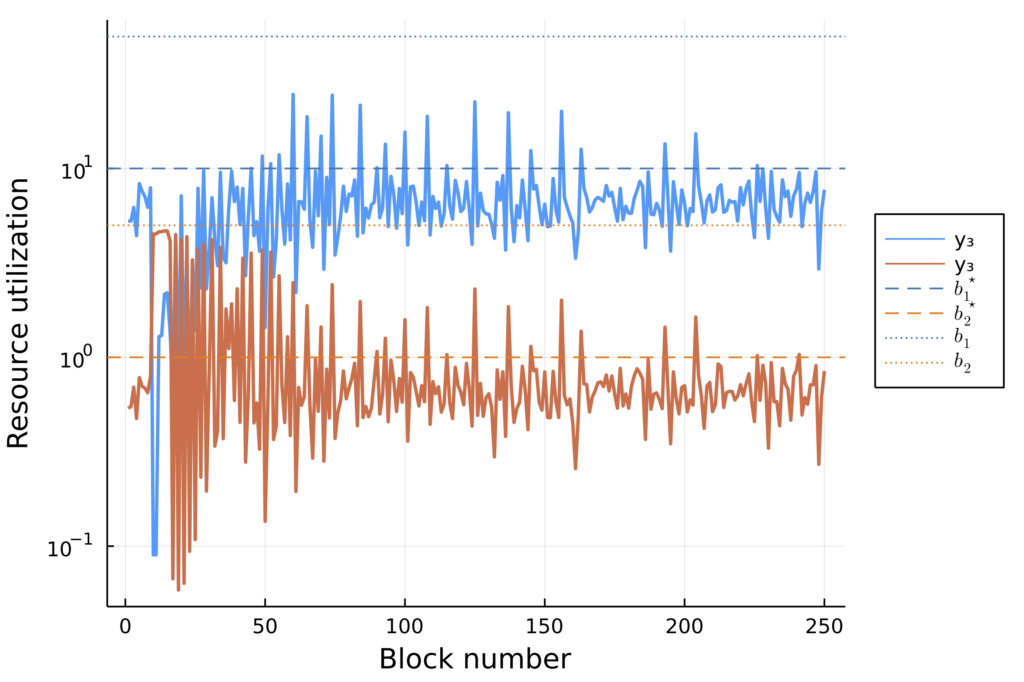
Looking at individual resource usage, we see that multidimensional pricing (left) facilitates smooth, short burst capacity, whereas uniform pricing (right) does not.

Implications and future work

We developed a general framework for multi-dimensional resource pricing in blockchains. While this work is a first step, there’s still plenty of work to do. Future research might include game-theoretic analyses of this mechanism along with more extensive numerical evaluation under realistic conditions. Still, we hope that our work helps base layer blockchain designers, rollup engineers, and application developers optimize fees at all layers of the decentralized stack as they design increasingly complex and performant systems.

For more details, please check out our paper!

Share
Contents