What happens when exchanges operate with a discrete clock? In our last post, we argued that blockchains have a system clock—the blocktime—and, therefore, should not permit events on a finer-scale resolution. We showed that this design choice prevents sandwich attacks, a harmful form of price manipulation on decentralized exchanges. But traders want more than to avoid a bad price; they want a good price.
Discrete-time, batched exchanges on public blockchains offer even more: they allow us to prove that a trade was executed at the best price given liquidity on all public markets.
Best Execution
Financial regulation widely recognizes principal-agent risk in markets with trusted intermediaries (such as brokers). To address this risk, these intermediaries are subject to a duty of best execution, which can generally be understood as “the duty to execute promptly, the duty to execute in an appropriate market, and the duty to obtain the best price.” [1] Although the specific compliance requirements may vary by jurisdiction, most financial regulatory regimes have the concept of “best execution,” and the principle has roots in common law agency principles and fiduciary duties.
Unfortunately, measuring whether investors received “best execution” in practice has been a challenge. As one article put it “best execution is easily defined but is often unrecognizable.” [2] We’d argue that recognition challenges stem from the lack of transparency and limited interoperability in traditional financial markets.
Under federal securities laws in the U.S., for example, “best execution” is not defined by statute or in an SEC rule. Originally derived from common law, it has generally been understood to be a duty on brokers to obtain the most favorable terms reasonably available under the circumstances for their customers’ orders. [3] As securities markets began to grow larger and more complex, however, there have been numerous attempts over the years to ensure investors actually receive best execution. The Securities Act Amendments of 1975 established a “national market structure” (NMS) to ensure that investors had access to the best prices across exchanges and trading venues. The market structure reforms in the early 2000s and the adoption of Regulation NMS were intended to improve disclosures around order execution quality and routing practices of brokers. And the SEC’s proposed (but not adopted) Regulation Best Execution in 2022 would have required brokers to establish more robust policies to ensure compliance with the standard. Despite years of good faith attempts, there is still no clear way to verify that an order received “best execution” in traditional markets.
Asset prices on a blockchain
Public blockchains, on the other hand, allow us to rigorously compute the “best price” for a particular trade. Decentralized exchanges have a public state that updates in discrete time. Each time the corresponding blockchain updates its state, the liquidity and prices on every decentralized exchange also update. In batched exchange designs, we can determine a single, unique price for each asset in each time period.
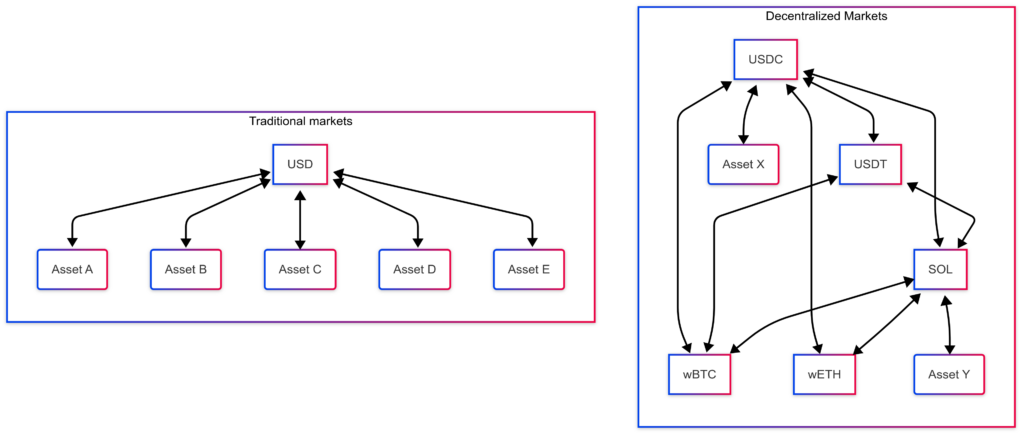
How do we compute the price of an order? Let’s consider an order to buy 100,000 SOL on the Solana blockchain with USDC. Our first instinct might be to find the most liquid SOL-USDC market and see what the price is there. But there are multiple stablecoins equivalent to USD on Solana. We could get a better price by converting some of our USDC into USDT and then using a SOL-USDT market as well. In addition, there are multiple decentralized exchanges to choose from. We likely need to split our order across all of these markets to get the best price.
But it gets more complicated! Perhaps the SOL-wBTC market is very liquid. We may consider first buying some wBTC with USD, and then buying SOL with wBTC. And so on. There’s a huge number of “paths” from USDC to SOL. This situation differs from traditional equities markets, where most assets are only paired with USD [4]. We want to find the best possible trade over all of these paths. We call this the routing problem.
Provable best price
We can not only efficiently solve the routing problem but also provide a mathematical certificate that we found the best possible route using convex optimization [5]. This certificate allows anyone to easily verify, given the previous state of the system, that a trade was in fact optimal. This means that batched decentralized exchanges can prove that they executed all received orders—aggregated together into a batched order—at the best possible price [6].
A blockchain’s public, discrete time nature is essential for this proof. The batched nature of orders ensures none of the manipulative behavior we’ve talked about previously interferes with the execution price.
Best (price) execution
Now we have a mathematical certificate of best price execution given liquidity across all markets on a particular public blockchain. It doesn’t matter how these markets are implemented; they can be automated market makers, order books, or something else. This certificate fulfills one of the goals of best execution: (provable) best price. Furthermore, this ability to compute the best price clarifies tradeoffs between price and other factors, like speed of execution.
Markets should have provable guarantees. We now have the technology to build this future.
Acknowledgements
We thank Alex Evans and Eric Budish for helpful comments on a draft of this post.
Footnotes:
[1] Francis J. Facciolo, A Broker’s Duty of Best Execution in the Nineteenth and Early Twentieth Centuries, 26 Pace L. Rev. 155 (2005), citing Norman Poser, Broker-Dealer Law & Regulation § 2.03[A], at 2-56 (3d ed. 2001).
[2] Id. citing Jonathan R. Macey & Maureen O’Hara, The Law and Economics of Best Execution, 6 J. Fin. Intermediation 188, 189 (1997).
[3] Newton v. Merrill, Lynch, Pierce, Fenner, 135 F.3d 266 (3d Cir. 1998).
[4] To exchange stock A for stock B in the traditional equities market, we first sell stock A and then use the proceeds from the sale (i.e., dollars or another currency) to buy stock B.
[5] In this case, the certificate is the list of post-trade, “market clearing prices” for all assets. One verifies this certificate by checking that these prices are in the no arbitrage interval for all markets.
[6] We don’t discuss issues of censorship here but recognize that it can be an issue in these systems.
 Skip to content
Skip to content
